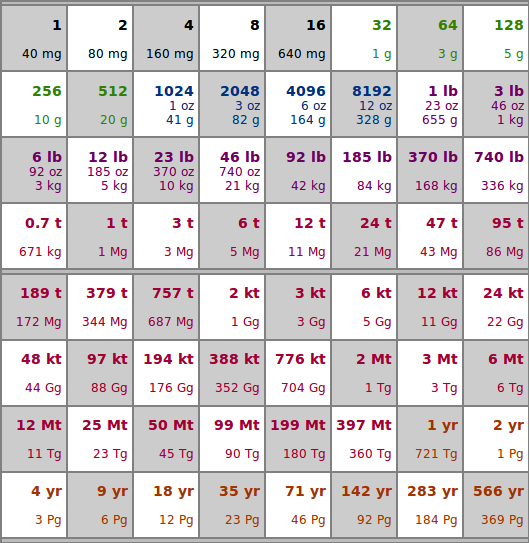
Mass-ive Exponental Growth
Wheat on a Chessboard — Calculated in Terms of Mass
February 6, 2017, John Æonid
I have long been fascinated with the difficulty we have dealing with the very large and the very small. Our limited working memory can only hold so many chunks of information, and we end up using abstractions to refer to things that are too big or too small to deal with. But, abstractions can lose their sense of proportion.
About a decade ago, I started playing with the “wheat on a chessboard problem”. One thing I noticed is that virtually all of the depictions I've seen only work with numbers, digits, or exponents. But, people already have trouble with numbers. So to make the quantities more palpable, I decided to work it out in mass (~weight).
- First quarter of chessboard: ranges from that first, single grain to over a kilogram or several pounds. Imagine a five-pound bag of flour (a bit under 3kg).
- Second quarter of chessboard: would fill more than a few tractor-trailer trucks (based on 50-ton capacity, dry-bulk semi-trailers).
- Third quarter of chessboard: in its middle has the mass of what would be carried by a container ship and ends with the 2010 annual wheat production of Brazil. *
- Fourth quarter of chessboard: contains over a millennia of wheat production—at the 2010 rate—for the entire World. *
So, imagine trying to balance a semitrailer on a chessboard, which is only in the second quarter of the chessboard. And, then imagine trying to balance a cargo ship on a chessboard. How would you do that? Yet, that's only the middle of the third quarter of the chessboard.
Ultimately, because of the way this works, that last quarter essentially represents the majority of entire chess board. (Note that a funny property of this chessboard problem is that each square contains exactly on more grain than the sum of all the squares before.) The first three quarters, at about 12 megatons, is just a drop in the bucket. Switching to using the World wheat production of 2010 as a unit of measure made the numbers much more comprehensible—if you can call it that. And given that this convenient unit is only one data point in an exponential growth over millenia, it may well be that this is more wheat than the total of all wheat that has ever been cultivated on this planet. Anybody care to estimate that? Mass-ive! (Seriously, massive, massive, massive)
Note that this is an image captured from an HTML table. I don't normally like to use an image where HTML/CSS would be better, but I dicided not to shoehorn the HTML/CSS code into this web-page builder.
March 4, 2018: Added image and coment, and revised text in first and last paragraphs.